
In other words, we assume that (a,b) is given and compute the position (u,v) as a function of x. Now that we know Snell's law for curves, we can turn the reflection law around and ask for the direction of a ray that reflects off a curve when it is emitted from a given point. Use these formulas to show that Fermat's least time principle implies Snell's law of equal angles of incidence and reflection for curved mirrors.You can study this formula in Chapter 15 of the text, or just use it now.Īpplying this formula to the angles between the tangent vectorĪnd each of the vectors from P to (x,f),, and (x,f) to Q,, gives the cosines of the angles, In order to easily interpret this formula, we need the fact that the cosine of the angle between two vectors To minimize t, we begin by computing critical points, (by the length formula or Pythagorean theorem), so the time required for light to pass along the path is A light ray hitting the graph at (x,f) is shown in Figure 27.5. Now we reflect light off a curved mirror.įor simplicity, we assume that the mirror is in the shape of a graph y=f. Prove thatĥ) Prove Snell's law, that the shortest reflected path makes i=r. Show that the total time required for a ray of light to travel this path isįigure 27.3: Coordinates for the Path of Lightĥ) The angles of incidence and reflection at (x,0) are shown on Figure 27.4. Similarly, the time required to go from (x,0) to (u,v) is that distance over c. Place coordinates on Figure 27.1 above so that the mirror forms the x-axis.ġ) Use the Pythagorean theorem to show that the length of the line segment from (a,b) to the reflection point (x,0) isĢ) Use the Pythagorean theorem to show that the length of the line segment from (x,0) to (u,v) isģ) Light travels at speed c, so the time required for light to go from (a,b) to (x,0) is the distance over c. We need to formulate the problem analytically. In other words, Fermat's principle implies Snell's law.īefore we move on to study reflection off curved mirrors, it is worthwhile to give a calculus proof of the shortest path. In other words, P to R to Q is the shortest reflected path.įigure 27.2: Proof of Snell's law for a Flat Mirrorįinally, light travels at constant speed c in air, so the shortest path is fastest and Fermat's principle says light must reflect at the point R that makes i=r. Since these segments form the sides of a triangle with P'Q as a base, P'S+SQ>P'Q.
ANGLE OF INCIDENCE EQUALS ANGLE OF REFLECTION PLUS
The distance traveled by light going from P to S is the same as that traveled by light going from P' to S by similar triangles, so the distance traveled by light going from P to S and then to Q is the sum of the two lengths P'S plus SQ. Since the angles i and r are equal, the points P', R, and Q lie on a line.īy similar triangles, the distance traveled by light going from P to R is the same as that traveled by light going from P' to R, so the distance traveled from P to R to Q is the length of P'Q. We will show that the time required for light to travel from P to Q through S is more than the time required to travel from P to Q through R, where i=r as shown in Figure 27.1.Ĭonstruct the point P' an equal distance below the mirror on a line normal to the mirror. To show that Fermat's principle gives Snell's law, suppose light reflected at a different point S on the mirror. In other words, Fermat's principle implies Snell's law. The angle of reflection is r between the normal and the outgoing ray of light.įigure 27.1: Snell's law, Angle of Incidence, i=r, Angle of Reflectionįermat gave a more general variational principle governing the path of light.įermat's principle says that light travels along the path that requires the least time.Īmong all paths reflected off a flat mirror, we can see geometrically that light will reflect at the point where the angle of incidence equals the angle of reflection.

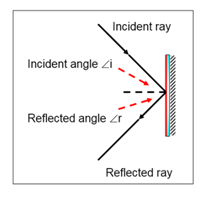
The angle of incidence is i between the incoming ray of light and the normal to the mirror. Snell's law from optics says that light traveling from point P to point Q reflects off a mirror so that the angle of incidence equals the angle of reflection. Calculus: Project 27 Project 27: Fermat's principle Implies Snell's law


 0 kommentar(er)
0 kommentar(er)
